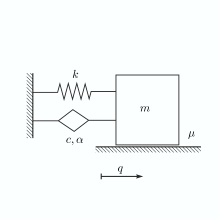
Fractional dynamical systems are described by differential equations with derivatives of arbitrary (non-integer) order. Among many other applications, the associated theory has been used in rheology to describe viscoelastically damped systems. Time-fractional elements, so called “springpots”, are used together with classical springs and dashpots to describe the viscoelastic behaviour on both short and long time-scales.
The aim of the project is to develop a Lyapunov stability theory for mechanical systems which have viscoelastic damping modelled by springpot-elements and, in addition, dry friction elements (i.e. set-valued Coulomb friction). First, we examine the physical meaning of fractional elements in mechanical systems and determine the (conserved and lost) energy of springpots which is needed to formulate Lyapunov functions for fractionally damped systems. Subsequently, we try to extend this framework to differential inclusions with fractional derivatives. The developed theory will be used to investigate dynamic instability problems in which damping plays an essential role (e.g. Ziegler’s paradoxon).
Another aspect of interest is the description of viscoelastically damped systems by differential equations containing variable-order fractional derivatives. We investigate the use of this approach to model the long-term behaviour of certain materials under stress by taking the example of salt concrete. Therefore, we want to develop time-dependent fractional models that characterize associated creep and relaxation processes and validate these models by experimental data.
Journal articles
- Hinze, M., Schmidt, A., & Leine, R. I. (2021). Finite element formulation of fractional constitutive laws using the reformulated infinite state representation. Fractal Fractional, 5, Article 132. https://doi.org/10.3390/fractalfract5030132
- Hinze, M., Schmidt, A., & Leine, R. I. (2020). The direct method of Lyapunov for nonlinear dynamical systems with fractional damping. Nonlinear Dynamics, 102, 2017–2037. https://doi.org/10.1007/s11071-020-05962-3
- Hinze, M., Schmidt, A., & Leine, R. I. (2020). Lyapunov stability of a fractionally damped oscillator with linear (anti-)damping. International Journal of Nonlinear Science and Numerical Simulation, 21, Article 5. https://doi.org/10.1515/ijnsns-2018-0381
- Hinze, M., Schmidt, A., & Leine, R. I. (2019). Numerical solution of fractional-order ordinary differential equations using the reformulated infinite state representation. Fractional Calculus and Applied Analysis, 22, Article 5. https://doi.org/10.1515/fca-2019-0070
Proceedings
- Hinze, M., Schmidt, A., & Leine, R. I. (2019). Numerical simulation of fractionally damped mechanical systems using infinite state representation. Proceedings of the 2019 International Conference on Fractional Calculus Theory and Applications (ICFCTA 2019).
- Hinze, M., Schmidt, A., & Leine, R. I. (2018, August). Mechanical representation and stability of dynamical systems containing fractional springpot elements. Proceedings of the ASME 2018 International Design Engineering Technical Conferences (IDETC2018), Article DETC2018–85146. https://doi.org/10.1115/DETC2018-85146
Contact

Remco I. Leine
Prof. Dr. ir. habil.director