Time finite element methods for nonsmooth mechanical systems

Since the introduction of finite element techniques in the early 1960s, these methods became indispensable for engineering development. The finite element procedures are employed extensively in the analysis of solids and structures, of heat transfer, and even in fluid mechanics. The algorithms used for the nonlinear finite element analysis of solids and structures are known to be very performing in terms of accuracy and robustness. These properties follow from the fact that the finite element description is derived from a variational formulation in the space dimension, e.g. the weak variational form of the principle of virtual work.

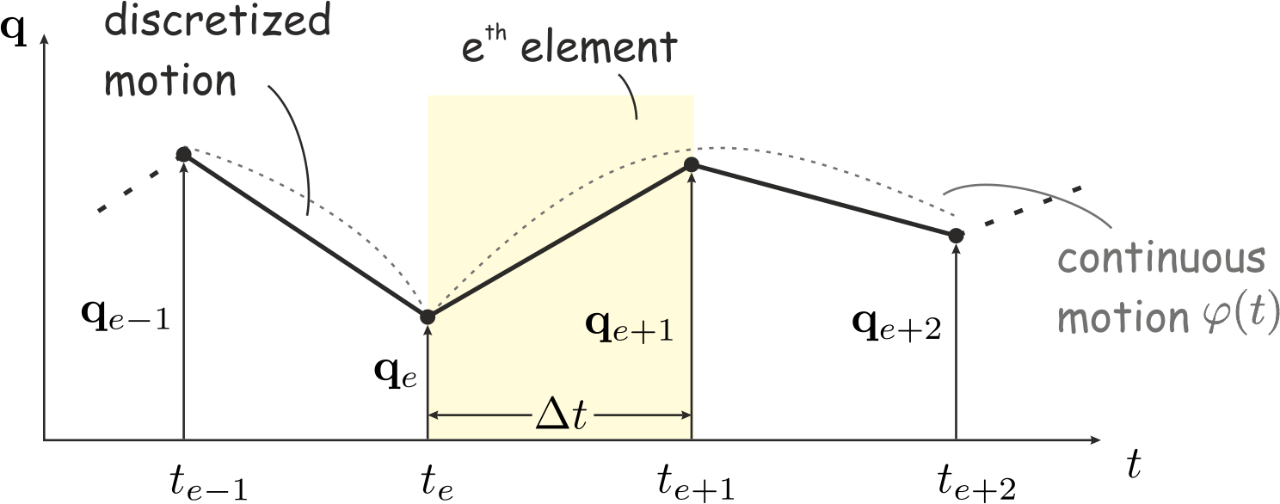
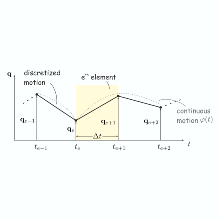
The aim of this project is to derive numerical time integration schemes for nonsmooth mechanical systems based on temporal finite element discretizations of variational formulations in time. Such variational formulations of mechanical systems are for instance the principle of virtual action or Hamilton’s principle. The main focus in this project lies in the treatment of constraints in a nonsmooth setting. The force laws belonging to such constraints are commonly formulated as normal cone inclusions. These force laws can describe constraints which are bilateral, unilateral, and possibly include friction. The strict satisfaction of unilateral constraints or certain frictional behavior can cause discontinuities in the velocities or in the accelerations. Impact laws are therefore required in the nonsmooth framework, which relate pre- and post-impact velocities with the contact efforts. For each instant of time, i.e. in a point wise manner, the concepts of contact and impact laws are very well understood. In order to deduce numerical schemes from a discretization of a variational formulation in time, also the contact and impact laws have to be embedded suitably in such a variational formulation. The following question arises. How can contact and impact laws be formulated, which are smeared over time and which represent the contact and the impact behavior of a finite time interval? Certainly, in the limit to infinitely small time steps, classical impact and contact formulations have to result.

Publications�

Capobianco, G., Eugster, S.R.:  “Time finite element based Moreau-type integrators”, International Journal for Numerical Methods in Engineering, pp. 1-17, published online, 2018. PDF INTJNUMERMETHENG

Capobianco, G., Winandy, T., Eugster, S.R., Leine, R.I.: “Comparison of Moreau-type integrators based on the time finite element discretization of the virtual action”, In Proceedings of the 9th European Nonlinear Dynamics Conference, pp. 1-2, 2017.  PDF

Capobianco, G., Eugster, S.R.: “A Moreau-type variational integrator”, In Proceedings in Applied Mathematics and Mechanics. 4 pages, submitted 2016.  PDF

Capobianco, G.: "Time Finite Element Methods for Mechanical Systems in Minimal Coordinates", Universität Stuttgart, Institut für Nichtlineare Mechanik (2015), Masterthesis. PDF
DOI: http://dx.doi.org/10.3929/ethz-a-010554060