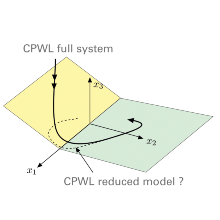
Piecewise linear (PWL) systems constitute an important class of nonsmooth dynamical systems and are commonly used to model complex physical phenomena. Typical applications are found in a wide range of fields, such as control systems, neuroscience and mechanical engineering. For instance, the presence of effects such as dry friction, intermittent contact or bilinear stiffness characteristics yields PWL mechanical models consisting of multiple linear subsystems. Due to their nonsmoothness properties, the PWL dynamics can exhibit very interesting dynamical effects, which are impossible to observe in smooth systems.
Existing techniques to study PWL systems are either restricted to low dimensional systems or rely on smoothing techniques, which cannot always capture the nonsmooth nature of the dynamics. However, the analysis of real-world applications requires high dimensional multibody mechanical models, which in turn present an additional challenge to the study of the PWL dynamics.
In this project, we explore the extension of singular perturbation theory to PWL mechanical systems to obtain approximations of their invariant sets, on which the full dynamics can be approximated by an adequate reduced order model. The aim is to reduce the computational efforts while also providing an insight into the main features of the global PWL dynamics.
Publications
- Karoui, A. Y., & Leine, R. I. (2025). Extended invariant cones as Nonlinear Normal Modes of inhomogeneous piecewise linear systems. International Journal of Non-Linear Mechanics, 174. https://doi.org/10.1016/j.ijnonlinmec.2025.105072
- Karoui, A. Y., & Leine, R. I. (2023). Model reduction of a periodically forced slow–fast continuous piecewise linear system. Nonlinear Dynamics. https://doi.org/10.1007/s11071-023-08858-0
- Karoui, A. Y., & Leine, R. I. (2022, July). Analysis of a singularly perturbed continuous piecewise linear system. Proceedings of the 10th European Nonlinear Dynamics Conference (ENOC2020+2). https://enoc2020.sciencesconf.org/394804
Kontakt

A. Yassine Karoui
M.Sc.
Remco I. Leine
Prof. Dr. ir. habil.Direktor