The concept of NNMs can be regarded as a nonlinear extension of modal analysis, which is presently a standard tool for numerical and experimental investigation of linear dynamic structures. However, most real life structures behave in a nonlinear way. For example, joints or large deformation in certain parts of the structure cause a nonlinear response. The numerical calculation of NNMs as well as the experimental identification is still a challenging task.
The overall dynamics of vibrating structures is significantly affected by local nonlinear elements.
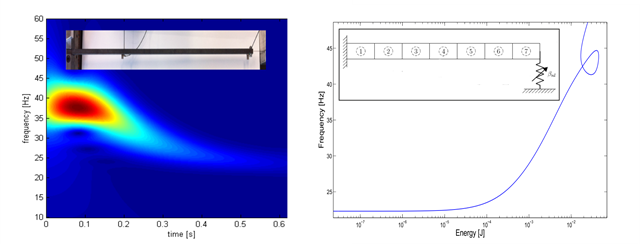
In contrast to linear systems, which have fixed eigenfrequencies being independent of vibration amplitudes, nonlinear systems show a more complex response. The nonlinear extension of eigenfrequencies of undamped nonlinear oscillators, which may be called nonlinear resonance frequencies, depend on the vibration amplitude. Furthermore, coupling effects between modes, or multiple stable and unstable periodic solutions at certain resonance frequencies, are induced by the nonlinearity. Many of these effects can be explained through NNMs. Also the experimental investigation of NNMs requires different techniques for measurements and analysis as compared to linear systems.
In addition, the extension of the concept of NNMs to weakly damped systems and its application to the calculation of limit cycles of self-excited vibrations which cause for example squealing noise in disc brakes is an interesting challenge.
Publications
Scheel, M., Peter, S., Leine, R.I. and Krack, M.: "A phase resonance approach for modal testing of structures with nonlinear dissipation", in Journal of Sound and Vibration, Vol. 435, pp. 56-73, 2018. PDF
Schreyer, F., Peter, S. and Leine, R. I.: “Experimental and Numerical Nonlinear Modal Analysis of a Beam with Impact: Part I – Numerical Investigation“, in Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics, Orlando, USA, 2018. PDF
Peter, S., Schreyer, F. and Leine, R. I.: “Experimental and Numerical Nonlinear Modal Analysis of a Beam with Impact: Part II – Experimental Investigation“, in Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics, Orlando, USA, 2018. PDF
Scheel, M., Kleyman, G., Tatar, A., Brake, M. R. W., Peter, S., Noël, J.-P., Allen, M. S. and Krack, M.: “System Identification of Jointed Structures: Nonlinear Modal Testing vs. State-Space Model Identification“, in Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics, Orlando, USA, 2018. PDF
Peter, S., Scheel, M., Krack, M. and Leine, R.I.: "Synthesis of nonlinear frequency responses with experimentally extracted nonlinear modes", in Mechanical Systems and Signal Processing, Vol. 101, pp. 498-515, 2018. https://doi.org/10.1016/j.ymssp.2017.09.014
Peter, S. and Leine. R.I.: "Excitation power quantities in phase resonance testing of nonlinear systems with phase-locked-loop excitation", in Mechanical Systems and Signal Processing, Vol. 96, pp. 139-158, 2017. https://doi.org/10.1016/j.ymssp.2017.04.011
Peter, S., Riethmüller, R. and Leine, R.I.: "Tracking of Backbone Curves of Nonlinear Systems using Phase-Locked-Loops" in Nonlinear Dynamics, Volume 1, Proceedings of the 34th IMAC, A Conference and Exposition on Structural Dynamics, 2016, Eds. Kerschen, G., Conference Proceedings of the Society for Experimental Mechanics Series, Springer. PDF
Peter, S., Grundler, A., Reuss, P., Gaul, L. and Leine, R. I. : "Towards Finite Element Model Updating Based on Nonlinear Normal Modes" in Nonlinear Dynamics, Volume 1, Proceedings of the 33rd IMAC, A Conference and Exposition on Structural Dynamics, 2015, Eds. Kerschen, G., Conference Proceedings of the Society for Experimental Mechanics Series, Springer, Cham, pp. 209-217, 2016. PDF
Peter, S., Schreyer, F., Reuss, P. and Gaul, L. :"Consideration of local stiffening and clearance nonlinearities in coupled systems using a generalized Harmonic Balance Method", Proc. ISMA, Leuven, 2014. PDF
Contact

Remco I. Leine
Prof. Dr. ir. habil.director